Comment les valeurs de résistance ressemblent-elles aux montgolfières de l’armée française des années 1800 ?
Quelle est l’étrange relation entre les valeurs des résistances et les montgolfières déployées par l’armée française à la fin des années 1800 ?
Si vous êtes impliqué dans l’électronique depuis un certain temps, vous ne pensez probablement pas beaucoup aux différentes valeurs associées aux résistances. En comparaison, les nouveaux venus dans le domaine sont souvent perplexes quant à la raison pour laquelle nous avons des valeurs de résistance telles que 12 kΩ, 15 kΩ, 18 kΩ, 22 kΩ, 27 kΩ, 33 kΩ, 39 kΩ, etc. Alors pourquoi ne pas garder les choses simples et avoir juste dix kΩ, 20 kΩ, 30 kΩ, 40 kΩ, etc. ? Le raisonnement derrière cela est en fait assez intéressant, mais d’abord, considérons les bases.
Lorsque nous concevons un circuit électronique, après avoir effectué les calculs appropriés, nous pouvons décider que — dans un monde idéal — nous aimerions utiliser une résistance d’une valeur précise de xxx (où la lettre grecque Omega est utilisée pour représenter la résistance dans ohms).
Une approche consisterait à fabriquer à la main des résistances individuelles avec des valeurs spécifiques au fur et à mesure des besoins, mais cela coûterait cher et prendrait beaucoup de temps. L’alternative est d’avoir accès à des composants abordables, préfabriqués et prêts à l’emploi. Le problème ici est que les fabricants ne pouvaient pas créer et fournir toutes les valeurs imaginables et – même s’ils le pouvaient – les utilisateurs des résistances ne pouvaient pas se permettre d’acheter toutes ces pièces et n’auraient pas suffisamment d’espace pour les stocker.
La solution trouvée par l’industrie était d’adopter un ensemble de valeurs de résistance standard. Cela vient avec l’avantage supplémentaire de permettre aux utilisateurs de se procurer leurs résistances auprès de plusieurs fabricants. Mais maintenant, nous avons la question de savoir quelles valeurs de résistance doivent être incluses dans l’ensemble.
Maintenant, accrochez-vous à vos chapeaux car nous sommes sur le point de faire un voyage dans le temps. En 1877, un ingénieur militaire français appelé Charles Renard a été présenté avec un poseur. À cette époque, l’armée française disposait d’un tas (pas le terme technique) de montgolfières qu’elle utilisait pour espionner les positions ennemies et larguer des bombes sur quiconque critiquait la cuisine française. Avant que Renard n’apparaisse sur les lieux pour maintenir leurs ballons en l’air, l’armée a été obligée d’entretenir 425 cordes différentes, ce qui était un cauchemar logistique. Renard a été chargé de réduire en quelque sorte ce nombre à une quantité plus gérable.
Les gens comme Renard m’étonnent parce que je ne me voyais jamais concevoir ce qu’ils font. Dans ce cas, Renard s’est rendu compte que si un produit doit être fabriqué dans une gamme de tailles, une façon de minimiser le nombre de tailles différentes qui doivent être fabriquées ou conservées en stock est de les choisir de manière à ce qu’elles soient à peu près également espacées. sur une échelle logarithmique.
Dans le système de Renard, l’intervalle de 1 à 10 était divisé en 5, 10, 20 ou 40 étapes, que nous appelons maintenant les échelles R5, R10, R20 et R40. Commençons par l’échelle R5, qui peut être représentée mathématiquement comme suit :
dix(0/5) = 1
dix(1/5) = 1,584… ≈1,6
dix(2/5) = 2,511… ≈2,5
dix(3/5) = 3,981… ≈4,0
dix(4/5) = 6,309… ≈6,3
dix(5/5) = 10
Notez que, puisque ce schéma est basé sur une approche logarithmique, chaque nouveau nombre peut être généré en multipliant la valeur précédente par 10(1/5) = 1,584 et arrondir au besoin.
Une grande chose à propos de l’approche logarithmique est que nous pouvons la répéter décennie par décennie. L’exemple ci-dessus concernait la décennie 1 à 10, mais la même chose s’applique aux décennies 10 à 100, 100 à 1 000, 1 000 à 10 000, et ainsi de suite. Une autre caractéristique intéressante de cette approche logarithmique est que si nous décidons de passer à une échelle de résolution plus élevée, les valeurs de l’échelle de résolution inférieure apparaissent également dans l’échelle plus complète. Prenons par exemple l’échelle R10 :
dix(0/10) = 1 (Identique à l’échelle R5)
dix(1/10) = 1,258… ≈1,3
dix(2/10) = 1,584… ≈1,6 (comme pour l’échelle R5)
dix(3/10) = 1,995… ≈2,0
dix(4/10) = 2.511… ≈2.5 (Identique à l’échelle R5)
dix(5/10) = 3.162… 3.2
dix(6/10) = 3,981… ≈4,0 (comme pour l’échelle R5)
dix(7/10) = 5,011… 5,0
dix(8/10) = 6,309… ≈6,3 (Identique à l’échelle R5)
dix(9/10) = 7,943… ≈7,9
dix(10/10) = 10 (Identique à l’échelle R5)
Dans ce cas, chaque nouveau nombre peut être généré en multipliant la valeur précédente par 10(1/10) = 1,258 et arrondir au besoin. La meilleure façon de comprendre cela si vous êtes débutant est au moyen d’une représentation graphique, comme indiqué ci-dessous.
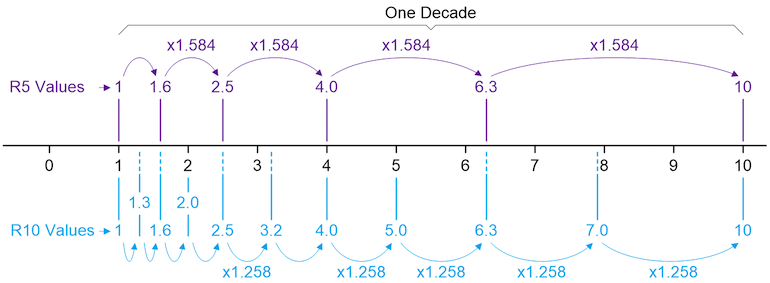
Une représentation graphique des échelles R5 et R10.
Comme nous l’avons mentionné précédemment, avant l’arrivée de Renard sur les lieux, l’armée française était obligée d’entretenir 425 cordes de tailles différentes afin de maintenir ses montgolfières en l’air. Après que Renard eut déterminé ses valeurs préférées basées sur des échelles logarithmiques, ce nombre fut réduit à 17 seulement, faisant de lui le « toast de la ville » vis-à-vis des intendants de l’armée. (C’est triste à dire, Renard ne devait plus jamais être invité à une soirée organisée par la guilde des cordiers.)
Les échelles R5, R10, R20 et R40 de Renard ont été officiellement adoptées comme normes par l’Organisation internationale de normalisation (ISO) au début des années 1950 et sont utilisées par diverses disciplines. Dans le cas de l’électronique, par exemple, ils sont utilisés pour des applications telles que le courant nominal des fusibles électriques et la tension nominale des condensateurs (par exemple, 100 V, 160 V, 250 V, 400 V, 630 V).
Cela dit, les échelles de Renard ne sont pas utilisées pour les résistances. En 1952, la CEI (Commission électrotechnique internationale) a défini un ensemble de valeurs standard pour différents types de composants, dont les résistances. Collectivement appelées « séries E », il s’agit en fait des séries E3, E6, E12, E24, E48, E96 et E192, où le nombre après le « E » désigne la quantité de « étapes » de valeur dans chaque série. . Dans le cas de la série E12, par exemple, cela pourrait être représenté mathématiquement comme suit :
dix(0/12) = 1
dix(1/12) 1.2
dix(2/12) 1.5
dix(3/12) 1,8
dix(4/12) 2.2
dix(5/12) 2,7
dix(6/12) 3.3
dix(7/12) 3.9
dix(8/12) 4.7
dix(9/12) 5.6
dix(10/12) 6,8
dix(11/12) 8.2
dix(12/12) = 10
Dans ce cas, chaque nouveau nombre peut être généré en multipliant la valeur précédente par 10(1/12) = 1.2115… 1.21. De plus, en gardant à l’esprit que ces valeurs se répètent chaque décennie, nous pouvons les résumer dans un tableau comme indiqué ci-dessous.

Une représentation tabulaire des valeurs de résistance E12 en ohms.
En ce qui concerne les valeurs indiquées comme 3R9, 3K9 et 3M9 dans le tableau ci-dessus, c’est juste une autre façon de dire 3,9 , 3,9 KΩ et 3,9 MΩ, respectivement. Le problème avec l’utilisation des points décimaux est qu’ils peuvent être facilement omis et/ou ils peuvent devenir obscurcis dans les documents imprimés, auquel cas 3,9 , 3,9 kΩ et 3,9 MΩ pourraient facilement être confondus avec 39 Ω, 39 kΩ et 39 MΩ, respectivement.
En conclusion, et pour répondre à notre question initiale, il devient maintenant clair pourquoi nous travaillons avec des valeurs de résistance telles que 12 kΩ, 15 kΩ, 18 kΩ, 22 kΩ, 27 kΩ, 33 kΩ, 39 kΩ, etc. Comme toujours, j’attends vos commentaires, questions et suggestions.







